karambola – morphometry.org

Karambola is a program to calculate irreducible (spherical) Minkowski Tensors and cartesian Minkowski Tensors of three-dimensional bodies and surfaces. The surface has to be given in terms of planar and convex polygons in the .poly file format or the OFF file format.
Minkowski Tensors can be calculated globally, or for subsets (called ”labels”).
In the demo folder a program called “pointpattern2voronoi” is included, which calculates the Voronoi Diagram of a given point pattern.

Download:

The source code can be found on Github, or as a ZIP archive.

Karambola is written in plain ISO C++ and only needs the GNU Scientific Library to compile. It is available as Free Software under the terms of the GNU General Public License, Version 3 or later. It also includes a copy of Catch2 for unit testing.

Installation

To compile Karambola, use: make
You need the GSL library to compile Karambola: http://www.gnu.org/software/gsl/
(for example, the libgsl-dev or libgsl-devel package on Linux)

To run the test suite, use: make test

Usage

To start Karambola, use the following syntax:
karambola input-file.poly {--labels | --nolabels} [more options...]

You have to use one of the the label flags:
--no-labels to indicate that you want to ignore the labels in the input file, if there are any
--labels to indicate that you want to use the labels in the input file
(an error occurs if the file has no labels and the --labels option is set)

Karambola calculates a standard set of Minkowski Tensors. If you like to compute a single Tensor, you can use the --compute w??? option, i. e. --compute w102.

If you add the option --reference_centroid, the tensors are calculated in reference to the Minkowski Vectors to the and not in reference to the origin, i. e. the reference point for the Minkowski Tensor Wn20 is the corresponding center of gravity

(1) $\begin{equation*} C_n = \frac{W_n^{10} }{ W_n^{00} } \end{equation*}$

You can define the outputfoldername if you use the option
--output outputfoldername or -o outputfoldername

If this option is not set, Karambola creates a folder named inputfilename_mink_val into which the outputfiles will be written.

Output files

Karambola creates a folder named inputfilename_mink_val or if the --output option is set a user defined folder, into which the outputfiles will be written. In the following the different outputfiles are explained:

surface_props:
in this file are some statistics: the shortest edge, longest edge, smallest area and largest area and for every label whether the surface is closed, shared with other labels or open.
ATTENTION: relatively short edges or small faces in your data (of order 1e-15) may generate ERRORs in the results or unreliable data.
w000_w100_w200_w300:
this file stores the results for the scalar Minkowski functionals.
w010_w110_w210_w310:
this file stores the results for the Minkowski vectors.
w020, w120, w220, w320, w102, w202
this file stores the results for the Cartesian Minkowski tensors of rank 2.
w020_eigsys, w120_eigsys, w220_eigsys, w320_eigsys, w102_eigsys, w202_eigsys
this file stores the results for the eigenvalues and eigenvectors of the Cartesian Minkowski tensors of rank 2.
msm_ql:
this file stores the irreducible Minkowski structure metrics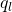 $q_l$ and $w_l$

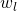
poly file format

A .poly file is a ASCII file that consists of two sections, separated by the keywords “POINTS”, “POLYS”, and “END”.

In the first section, the coordinates of each vertex are defined. Each vertex is introduced by positive and consecutive integers starting from 1 and a colon; coordinates are given as floating-point numbers.

The second section defines the actual polygons. Again, each polygon is introduced by a number, and a colon (:), followed by references to the vertices of the first section and the character “<“.

Note: Karambola can process convex polygons, which are triangulated in a simple way. The first vertex is connected to every other vertex of the polygon, so that you get n-2 triangles, where n is the number of vertices of a triangle. Non-convex polygons are not supported!

The normal of each polygon is provided by the order of the vertices and is defined by

(2) $\begin{equation*} \text{normal} = \frac{ (\text{vertex}_{i+1} - \text{vertex}_1) \times (\text{vertex}_{i+2} - \text{vertex}_1)} {|(\text{vertex}_{i+1} - \text{vertex}_1) \times (\text{vertex}_{i+2} - \text{vertex}_1)|} \quad , \quad i = 1,...,n-2 \end{equation*}$

‘ $\times$ ‘ indicates the cross product, and |.| indicates the Euclidean norm.

If your surface is the topological boundary of a set, all normals have to be inward-pointing or outer-pointing normals. If you mix them, the surface is detected as “open” and not all Minkowski Tensors can be calculated.

Labels (`--labels`)

It is possible to label the polygons by adding a “c” after the character “<“.
In the following parentheses, four numbers separated by a comma are needed.
The first three are not used, the last number has to be an integer and and is used for the label.
For each label, the Minkowski Tensors are calculated individually if the --labels option is used.
(an error occurs if the file has no labels and the --labels option is set).

Minimal example of a .poly file describing a triangle labelled with ’7’ and a triangle labelled with ’2’:

POINTS

1: 0.000000000e+00 0.000000000e+00 0.000000000e+00

2: 1.000000000e+00 0.000000000e+00 1.000000000e+00

3: 0.000000000e+00 1.000000000e+00 1.000000000e+00

4: 1.000000000e+00 1.000000000e+00 2.000000000e+00

POLYS

1: 1 2 3 < c(0 , 0 , 0 , 7)

2: 2 1 4 < c(0 , 0 , 0 , 2)

END

Look at the demo folder to find examples for poly files.

OFF file format

Detailed information about the OFF file format can be found here.

Minimal example of a OFF file describing a cuboid:

OFF

# comment: cuboid.off
8 6 12 # the file contains 8 points and 6 facets
# coordinates of points

 1.0   0.0   1.0

 0.0   1.0   1.0

-1.0   0.0   1.0

 0.0  -1.0   1.0

 1.0   0.0  -1.0

 0.0   1.0  -1.0

-1.0   0.0  -1.0

 0.0  -1.0  -1.0
# facets: number of vertices, followed by the indexes of the composing vertices, in order (indexed from zero).

# Optional: the RGB values for the face color can follow (ignored by karambola)

# Optional: after the RGB values follows the label of the surface.

4 0 1 2 3 255 0 0 1 4 7 4 0 3 255 0 0 1 4 4 5 1 0 255 0 0 1 4 5 6 2 1 0 255 0 2 4 3 2 6 7 0 255 0 2 4 6 5 4 7 0 255 0 2

Troubleshooting

there are more than one objects at vertex

At least one vertex in the poly shows the following situation:

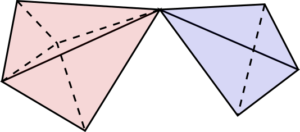
If two objects share a vertex, you have to double that vertex and use a different one for each object.
This needs to be done even if the two objects have different labels.

A discussion about how to fix such non-manifold vertices can be found here.

References

The code used in karambola is described in the following publications:
[bibtex key=schroder-turk2013minkowski,schroder-turk2011minkowski]