Point patterns can be analyzed using irreducible Minkowski tensors.
For the analysis, one constructs the Voronoi diagram with the point pattern as the Voronoi seeds. The Voronoi diagram is the collection of cells which tiles the plane and in which each point in the plane is assigned to the closest Voronoi seed.
Computing the irreducible Minkowski tensors of these cells, one can classify different types of local structures. In particular, the IMT 
is sensitive to local sixfold order which is typical in two dimensions. It can be visualized by coloring the cells according to the 
rotational invariant:
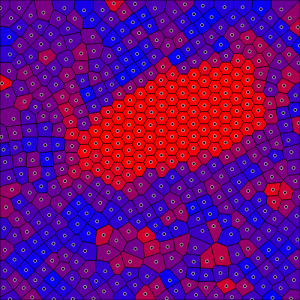(click here to this example in Morphometer)
In this mode of analysis, IMTs generalize Paul Steinhardt’s bond-orientational order parameters [bibcite key=steinhardt1983bond-orientational]. The nearest neighbors of a seed point are determined from the Voronoi diagram, and weighted according to the length of the interface between the two Voronoi cells [bibcite key=mickel2013shortcomings].