Minkowski scalars are robust and intuitive shape measures. For sufficiently smooth bodies ![]() , the Minkowski Scalars are just (weighted) integrals over the volume or boundary of the body
, the Minkowski Scalars are just (weighted) integrals over the volume or boundary of the body ![]() . There are three linearly independent Minkowski scalars in two dimensions, and four in three dimensions. Minkowski scalars are also known as intrinsic volumes.
. There are three linearly independent Minkowski scalars in two dimensions, and four in three dimensions. Minkowski scalars are also known as intrinsic volumes.
The Minkowski scalars can be interpreted as area, perimeter, and the Euler characteristic. The latter is a topological measure; for compact bodies it is given by the number of components minus the number of cavities. All three can be written as integrals, weighted (blue color) by the area, the contour length, and the local curvature of the contour:

Body

Area
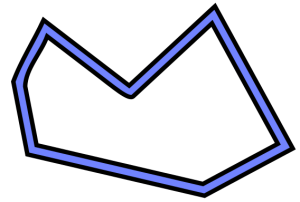
Perimeter

Euler characteristic
where ![]() is the curvature of the contour at point
is the curvature of the contour at point ![]() . The Euler characteristic is given by the number of components minus the number of cavities:
. The Euler characteristic is given by the number of components minus the number of cavities:

Hadwiger’s characterization theorem
Hadwiger’s characterization theorem [bibcite key=hadwiger1957vorlesungen] states that any additive, continuous, and motion-invariant functional ![]() of a convex body
of a convex body ![]() can be expressed as a linear combination of the
can be expressed as a linear combination of the ![]() Minkowski functionals
Minkowski functionals ![]() of the body
of the body ![]() :
:
(1) 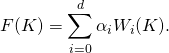
Here, ![]() are constants independent of
are constants independent of ![]() . The shape information about
. The shape information about ![]() is completely contained in the
is completely contained in the ![]() , which are
, which are ![]() ,
, ![]() , and
, and ![]() . In this sense, the Minkowski scalars are the relevant shape indices for physical functionals with the additivity property.
. In this sense, the Minkowski scalars are the relevant shape indices for physical functionals with the additivity property.