Anisotropy analysis by IMT – 3D

In three dimensions, irreducible Minkowski tensors (IMT’s) are defined by an expansion of the density of surface normal directions, in complete analogy to the two-dimensional case. The distribution of surface normals uniquely determines a convex object. (This statement is known as Minkowski’s problem. In this context, the surface normal density is sometimes called the extended Gaussian image. [bibcite key=horn1984egi])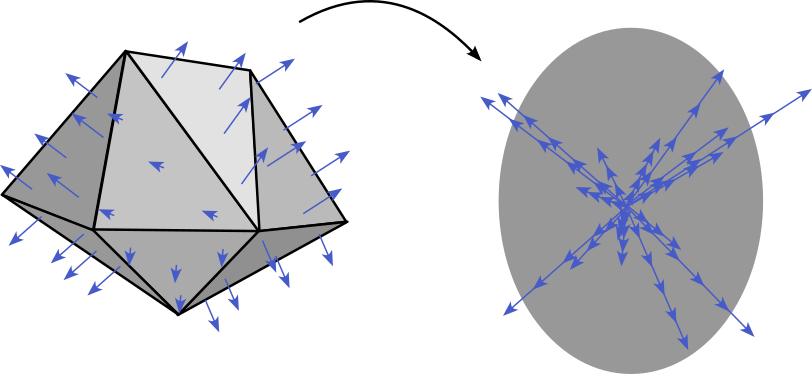

It is useful to select the complete orthogonal set of Spherical harmonics as basis functions. For a polyhedron with face areas $A_k$ and normals $\vec n_k$ , the IMT’s are given by

$\displaystyle \psi_{s,m} = \sum_k A_k Y_s^m(\vec n_k)$ .

Here $Y_s^m(\vec n)$ is the obvious notation for the spherical harmonic evaluated with the direction corresponding to the normal $\vec n$ . The index $s = 0, 1, 2, \dotsc$ labels increasing tensor ranks, and $m=-s, \dotsc, s$ is the “magnetic quantum number”. The complex coefficients $\psi_{s,m}$ have the usual transformation properties of spherical harmonics under rotations.

Often, it is useful to define rotational invariants which can serve as fingerprints of a body irrespective of its orientation in space. The quadratic invariants in particular are

$\displaystyle q_s = \frac{4\pi}{2s+1} \times \frac{1}{A} \times \sum_{m=-s}^s |\psi_{s,m}|^2$ .

For convenience, we have also divided by the total surface area, such that the $q_s$ are invariant under translation, rotation, and scaling.

Three-dimensional irreducible Minkowski Tensors are discussed in greater detail in Ref. [bibcite key=mickel2013shortcomings]. When computed for Voronoi cells, they generalize Paul Steinhardt’s bond-orientational order parameters [bibcite key=steinhardt1983bond-orientational].