Home
Welcome to morphometry.org
Minkowski scalars and tensors are a versatile, sensitive and robust way to quantify shape. Here, we present example applications to real world data and to mathematical models. You can explore the possibilities of these shape measures in our morphometer, an interactive sandbox. The theory section provides an accessible introduction to the rich mathematical background.
We hope you enjoy this website. If you have any questions or feedback, you can write to info@morphometry.org.
Sebastian Kapfer, Michael Klatt, Fabian Schaller, and Jenny Wagner
Software
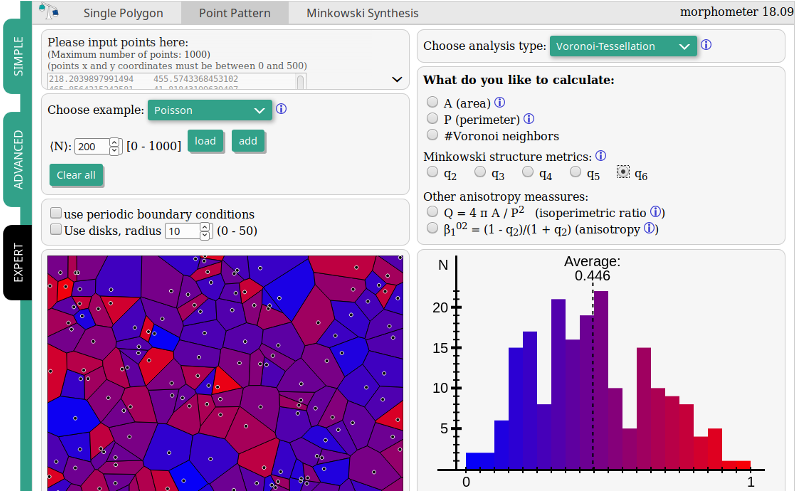
Morphometer, a 2D online tool to calculate Minkowski functionals of 2D point patters, single polygons and grayscale images is available now:
News
12.10.2020: Our article about papaya2 has been published in the Journal of Open Source Software!
09.10.2020: Morphometer 20.10 released.
03.10.2020: New examples online: Astronomical data analysis and Quasicrystal analysis.
29.08.2020: papaya2.js, the papaya2 javascript binding is online.
07.07.2020: OFF file support for karambola.
06.06.2020: papaya2 page contains library documentation.
01.04.2019: Morphometer 19.04 released: improved features and a distinguished directions analysis for single polygons and images.
08.03.2019: papaya2: A new C++ library for 2D point pattern and image analysis, including a python module and a Matlab extention
19.02.2019: Morphometer 19.02 released, includes grayscale image analysis.
24.09.2018: Minkowski synthesis available in morphometer 18.09.
03.09.2018: An accessible introduction to the anisotropy analysis by Irreducible Minkowski Tensors is available.
19.07.2018: Convex hull construction available in Morphometer.
27.02.2018: Stay updated by subscribing to the newsletter.
Acknowledgements
We thank the interdisciplinary research unit “Geometry and Physics of Spatial Random Systems” set up by the German Research Foundation (DFG) in February 2011. This unit comprises mathematicians from the Karlsruhe Institute of Technology, working on stochastic and integral geometry and spatial stochastics, theoretical physicists from the University of Erlangen-Nuremberg and Murdoch University in Perth, working on statistical physics of spatially complex and disordered materials, and the stochastic geometry group from the University of Aarhus, working on spatial statistics and image analysis. The research unit aims at building bridges between mathematics and physics and at exploring the geometry and physics of random structures in space.
We also thank the Institute of Stochastics at the Karlsruhe Institute of Technology, the Institute of Theoretical Physics at the University of Erlangen-Nuremberg and Murdoch University in Perth.