For sufficiently smooth bodies ![]() , the Minkowski Functionals can be intuitively defined via (weighted) integrals over the volume or boundary of the body
, the Minkowski Functionals can be intuitively defined via (weighted) integrals over the volume or boundary of the body ![]() .
.
The scalar functionals can be interpreted as area, perimeter, or the Euler characteristic, which is a topological constant. The vectors are closely related to the centers of mass in either solid or hollow bodies. Accordingly, the second-rank tensors correspond the tensors of inertia, or they can be interpreted as the moment tensors of the distribution of the normals on the boundary.
Minkowski Functionals
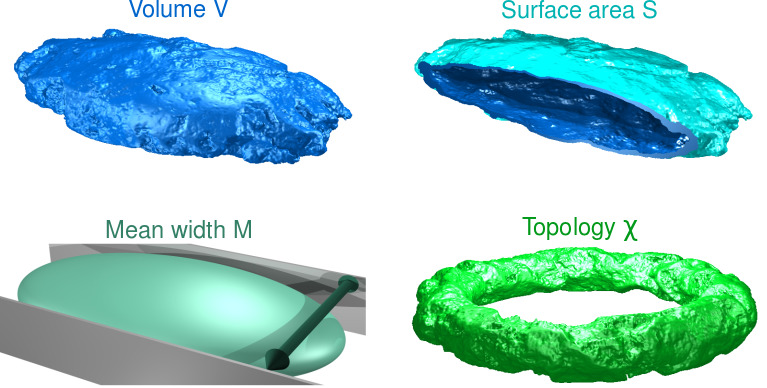
Volume
![]()
Surface area
![]()
Integrated mean curvature
(Mean width for convex bodies)
![]()
Euler Characteristic
![]()
with
![]()
![]()
![]() = principal curvature
= principal curvature
Cartesian representation (Minkowski Tensors)
Using the position vector ![]() and the normal vector
and the normal vector ![]() on the boundary, the Minkowski Vectors can be defined in the Cartesian representation.
on the boundary, the Minkowski Vectors can be defined in the Cartesian representation.
The second-rank Minkowski tensors are defined using the symmetric tensor product ![]() .
.
Minkowski Vectors
![]()
![]()
![]()
![]()
Minkowski Tensors
![]()
![]()
![]()
![]()
![]()
![]()
Figures are under construction
Irreducible representation (Spherical Minkowski Tensors)
under construction