2D Functionals

For sufficiently smooth bodies K, the Minkowski Functionals can be intuitively defined via (weighted) integrals over the volume or boundary of the body K.

The scalar functionals can be interpreted as area, perimeter, or the Euler characteristic, which is a topological constant. The vectors are closely related to the centers of mass in either solid or hollow bodies. Accordingly, the second-rank tensors correspond the tensors of inertia, or they can be interpreted as the moment tensors of the distribution of the normals on the boundary.

Minkowski Functionals

Area
W_0 = \quad \int\limits_K \mathrm d A \propto V_2
Perimeter
W_1 = \frac 12 \int\limits_{\partial K} \mathrm d l \propto V_1
Euler characteristic
W_2 = \frac 12 \int\limits_{\partial K} \kappa\, \mathrm d l \propto V_0

with
\kappa = curvature

Cartesian representation (Minkowski Tensors)

Using the position vector \textbf r and the normal vector \textbf n on the boundary, the Minkowski Vectors can be defined in the Cartesian representation.

The second-rank Minkowski tensors are defined using the symmetric tensor product (\textbf a\otimes \textbf a)_{ij} = a_i a_j.

Minkowski Vectors

W_0^{1,0} = \quad \int\limits_K \textbf r \, \mathrm d A\propto \Phi_2^{1,0}
W_1^{1,0} = \frac 12 \int\limits_{\partial K} \textbf r \, \mathrm d l\propto \Phi_1^{1,0}
W_2^{1,0} = \frac 12 \int\limits_{\partial K} \kappa \, \textbf r \, \mathrm d l\propto \Phi_0^{1,0}

Minkowski Tensors

W_0^{2,0} = \quad \int\limits_K \textbf r \otimes \textbf r \, \mathrm d A\propto \Phi_2^{2,0}
W_1^{2,0} = \frac 12 \int\limits_{\partial K} \textbf r \otimes \textbf r \, \mathrm d l\propto \Phi_1^{2,0}
W_2^{2,0} = \frac 12 \int\limits_{\partial K} \kappa \, \textbf r \otimes \textbf r \, \mathrm d l\propto \Phi_0^{2,0}
W_1^{0,2} = \frac 12 \int\limits_{\partial K} \textbf n \otimes \textbf n \, \mathrm d l\propto \Phi_1^{0,2}
W_2^{0,2} = \frac 12 \int\limits_{\partial K} \kappa \, \textbf n \otimes \textbf n \, \mathrm d l\propto \Phi_0^{0,2}

 

 

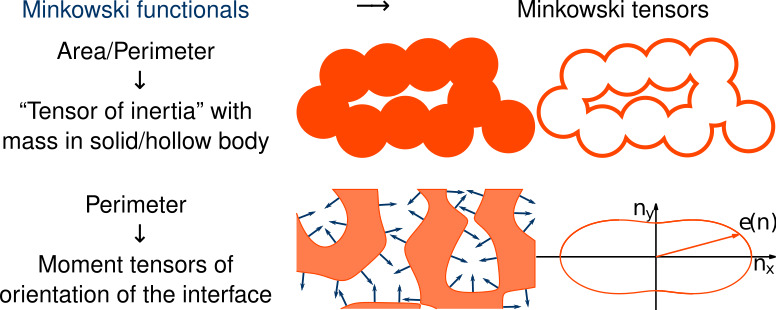
Irreducible representation (Circular Minkowski Tensors)

Due to the different rotational symmetries of, for example, a rectangle and a triangle, their anisotropy is encoded in Minkowski tensors of different rank, for example, in W_1^{0,2} for the rectangle and in W_1^{0,3} for the triangle. To define rotational invariants that quantify the degree of anisotropy of different ranks (different rotational symmetries), we need the irreducible representation. Loosely speaking, it is a decomposition into tensors with an s-fold rotational symmetries.

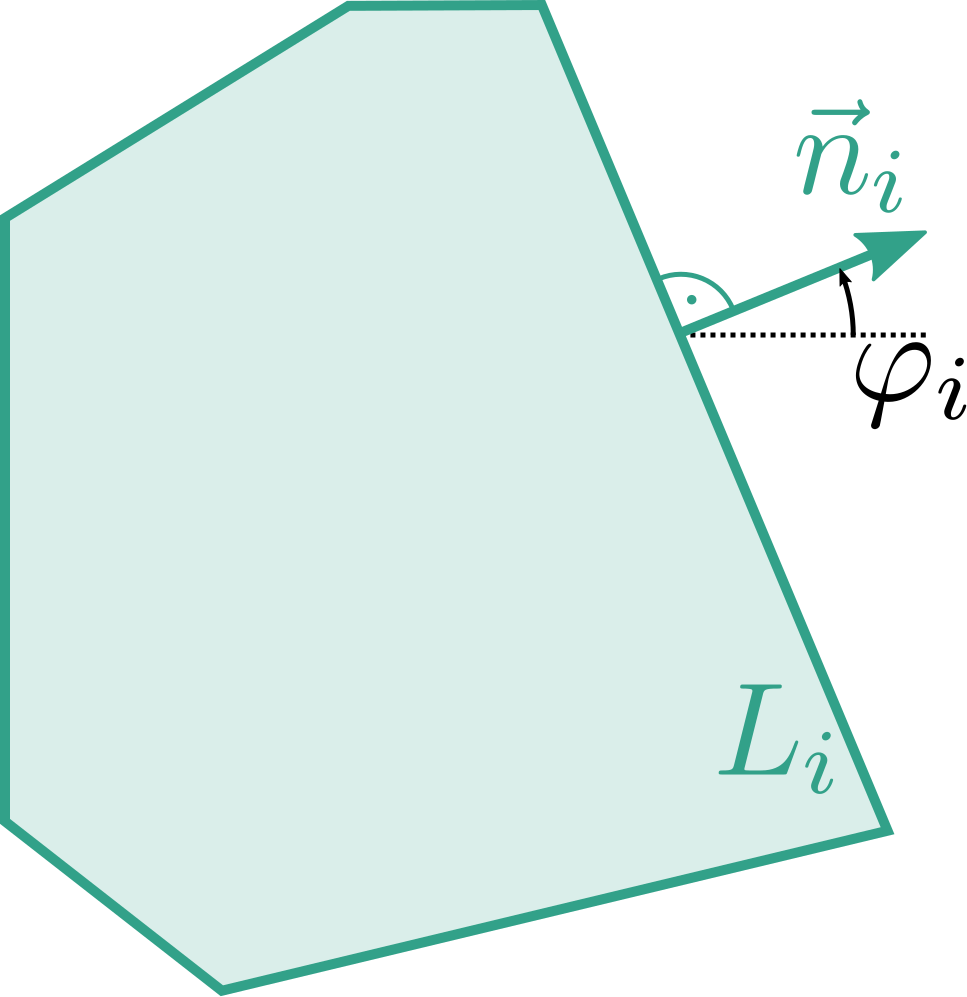
Consider a polygon with edge lengths L_i:
\vec L_i = L_i \cdot \vec n_i.

Density of normals:
\rho(\varphi) = \sum\limits_i L_i \, \delta(\varphi-\varphi_i)

Fourier analysis:
\psi_s = \int\limits_{0}^{2\pi} \textnormal d \varphi \,\textnormal{e}^{i s \varphi} \, \rho(\varphi) = \sum\limits_i L_i \, \textnormal{e}^{i s \varphi_i}

The zeroth Fourier component is the circumference of the polygon: \psi_0 = L = 2\,W_1
The first Fourier component vanishes for all closed polygons: \psi_1 = 0

The shape indices q_s are defined as

(1)   \begin{align*} q_s := \frac{|\psi_s|}{\psi_0} \end{align*}

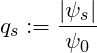
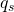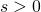All anisotropy indices q_s for s>0 vanish only for the circle (left). If there is only a single anisotropy index 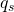q_s non-zero, the choice of this rank s defines a convex shapes with an s-fold rotational symmetry.

 

q_0 = 1
q_1 = 0 for closed polygons.
q_2 is the quadrupole component of the normal density, it is related to \beta_1^{0,2} - 1
q_3 can detect anisotropy in a three-fold symmetric system (e.g. suitable for detecting equilateral triangles)
q_4 can detect anisotropy in a four-fold symmetric system (e.g. suitable for detecting rectangles)
q_5 …

Morphometric distance

A morphometric distance of a polygon K to a reference structure R can be quantified by considering the pseudo distance function

d(K) = \sqrt{\sum\limits_l [q_l(K) - q_l(R)]^2}.