3D Functionals

For sufficiently smooth bodies K, the Minkowski Functionals can be intuitively defined via (weighted) integrals over the volume or boundary of the body K.

The scalar functionals can be interpreted as area, perimeter, or the Euler characteristic, which is a topological constant. The vectors are closely related to the centers of mass in either solid or hollow bodies. Accordingly, the second-rank tensors correspond the tensors of inertia, or they can be interpreted as the moment tensors of the distribution of the normals on the boundary.

Minkowski Functionals

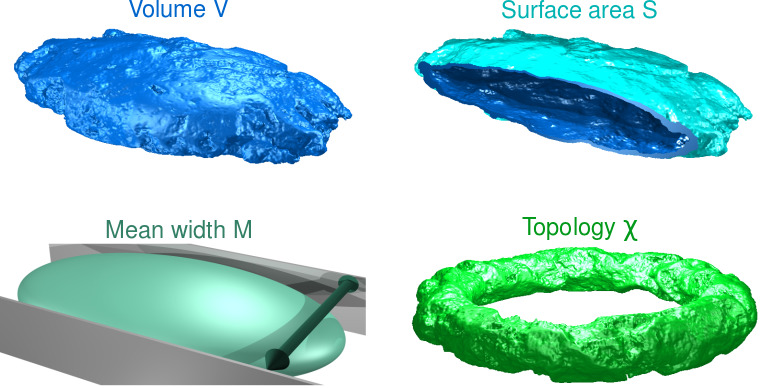
Volume
W_0 = \quad \int\limits_K \mathrm d V \propto V_3
Surface area
W_1 = \frac 13 \int\limits_{\partial K} \mathrm d \mathcal O \propto V_2
Integrated mean curvature
(Mean width for convex bodies)
W_2 = \frac 13 \int\limits_{\partial K} H \mathrm d \mathcal O \propto V_1
Euler Characteristic
W_3 = \frac 13 \int\limits_{\partial K} G \mathrm d \mathcal O\propto V_0

with
H= \frac 12 (\kappa_1 + \kappa_2)
G= \kappa_1 \kappa_2
\kappa_i = principal curvature

Cartesian representation (Minkowski Tensors)

Using the position vector \textbf r and the normal vector \textbf n on the boundary, the Minkowski Vectors can be defined in the Cartesian representation.

The second-rank Minkowski tensors are defined using the symmetric tensor product (\textbf a^2)_{ij} = a_i a_j.

Minkowski Vectors

W_0^{1,0} = \quad \int\limits_K \textbf r \, \mathrm d V\propto \Phi_3^{1,0}
W_1^{1,0} = \frac 13 \int\limits_{\partial K} \textbf r \, \mathrm d \mathcal O\propto \Phi_2^{1,0}
W_2^{1,0} = \frac 13 \int\limits_{\partial K} H \, \textbf r \, \mathrm d \mathcal O\propto \Phi_1^{1,0}
W_3^{1,0} = \frac 13 \int\limits_{\partial K} G \, \textbf r \, \mathrm d \mathcal O\propto \Phi_0^{1,0}

Minkowski Tensors

W_0^{2,0} = \quad \int\limits_K \textbf r \otimes \textbf r \, \mathrm d V\propto \Phi_3^{2,0}
W_1^{2,0} = \frac 13 \int\limits_{\partial K} \textbf r \otimes \textbf r \, \mathrm d \mathcal O\propto \Phi_2^{2,0}
W_2^{2,0} = \frac 13 \int\limits_{\partial K} H \, \textbf r \otimes \textbf r \, \mathrm d \mathcal O\propto \Phi_1^{2,0}
W_3^{2,0} = \frac 13 \int\limits_{\partial K} G \, \textbf r \otimes \textbf r \, \mathrm d \mathcal O\propto \Phi_0^{2,0}
W_1^{0,2} = \frac 13 \int\limits_{\partial K} \textbf n \otimes \textbf n \, \mathrm d \mathcal O\propto \Phi_2^{0,2}
W_2^{0,2} = \frac 13 \int\limits_{\partial K} H \, \textbf n \otimes \textbf n \, \mathrm d \mathcal O\propto \Phi_1^{0,2}

Figures are under construction

Irreducible representation (Spherical Minkowski Tensors)

under construction