None
Random point patterns can exhibit a rich variety of disordered structures, from the completely independent particle positions in an ideal gas to clustering point processes with strong fluctuations or to repulsive point patterns with an anomalous suppression of density fluctuations. These patterns can model particles in physics, galxies in the universe, nodes in telecommunication networks or trees in forests or galaxies, to name just a few applications. Formally speaking a point patterns is the realization of a point process. The complex structure of the random point patterns can be quantified either directly (e.g., by the exclusion probability or the correlation functions) or indirectly by constructing `secondary structures’ [bibcite key=”sonoda2008phase”] (Illian et al. 2008), including random fields (see shot-noise fields), random sets (see germ-grain models), networks or graphs (see Polygons), or tessellations (partitions of space into non-overlapping cells). Here we analyze 2D point/particle configurations via their so-called Voronoi or Delaunay tessellations. The user can choose in the Morphometer to just show the point pattern (no analysis is performed).
Voronoi tessellation
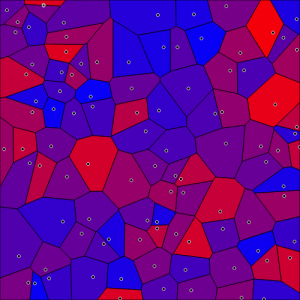
A Voronoi tessellation assigns to each point 
in the point pattern a convex cell that contains all sites 
that are closer to this point than to any other point 
in the point pattern. It is an intuitive `quantization’ of space into cells based on a (random) point pattern. Many rigorous and empirical results have been obtained for Voronoi tessellations, including inparticular the Minkowski functionals of the Poisson Voronoi cells. The distribution of the typical Voronoi cell characterizes the local `neighborhood’ of a typical point in the process. The Morphometer computes the histogram of the Minkowski tensors of the Voronoi cell for a point pattern chosen by the user.
Delaunay tessellation
The Delaunay tessellation is a triangulation, in which no point in the point pattern is inside the circumcircles of any of the triangles. While for crystalline point configurations the Delaunay triangulation may not be unique, for the realizations of typical point processes (like the ideal gas, that is, the Poisson point process) it is almost surely unique. In these cases it corresponds to the dual graph of the Voronoi tessellation. It can be constructed by first projecting the points onto a three-dimensional paraboloid, then constructing the convex hull in 3D, and finally projecting the facets of this convex hull back into the Euclidean plane. Like for the Voronoi tessellation, the Morphometer computes the histogram of the Minkowski tensors of the cells for a point pattern chosen by the user.